Sejak manusia mulai mempelajari astronomi, sudah banyak upaya dan cara dilakukan untuk menghitung jarak matahari dari planet bumi, dan sayangnya beberapa dari cara-cara tersebut mendapatkan hasil yang kurang tepat. Seperti cara perhitungan jarak matahari dari bumi yang dapat kita lihat di video tentang FE. FE melakukan perhitungan jarak matahari dari bumi dengan menggunakan metode bayangan dan trigonometri, seperti yg dilakukan ilmuan terdahulu Eratosthenes. Dari perhitungan tersebut, FE menyimpulkan bahwa jarak matahari dari bumi ialah sekitar 5000 sampai 6000 km. Dan ternyata hasil tersebut sangat jauh dengan kenyataan. Hal itu disebabkan asumsi FE yang keliru, yaitu datangnya sinar Matahari tidak sejajar sehingga membentuk sudut terhadap tongkat yang ditancapkan di tanah. Padahal sinar Matahari datangnya sejajar karena letaknya sangat jauh, dan akibatnya sudut yang terbentuk tersebut sebenarnya berasal dari kemiringan/kelengkungan bentuk permukaan Bumi.
Jarak matahari dari bumi merupakan hal yang sangat penting bagi dunia astronomi untuk dapat mempelajari banyak hal lain. Copernicus menyadari akan hal itu, dan menjelang tahun 1600 an, dia dan beberapa ilmuwan lain sudah mengetahui jarak relatif planet-planet di tata surya terhadap Matahari dengan dasar bahwa jarak Matahari dari Bumi adalah 1. Namun karena jarak Matahari dari Bumi belum diketahui, maka jarak semua planet juga belum diketahui secara detil. Berikut adalah data jarak planet-planet dari matahari dengan menggunakan SA (satuan astronomi), yakni jarak matahari dari bumi, sebagai acuan.
| Planet | Jarak dari Matahari |
| Merkurius | 0,38 SA |
| Venus | 0,723 SA |
| Bumi | 1,000 SA |
| Mars | 1,524 SA |
| Jupiter | 5,204 SA |
| Saturnus | 9,582 SA |
Pada tahun 1653, astronom bernama Christian Huygens memanfaatkan fase Venus yang tampak dari Bumi untuk menghitung jarak matahari dari bumi. Venus memiliki fase-fase selayaknya macam-macam fase Bulan dan bentuk fase tersebut erat kaitannya dengan sudut yang terbentuk antara Matahari-Venus-Bumi. Dan dari pengamatan di Bumi, Huygens bisa menghitung sudut yang terbentuk antara Matahari-Bumi-Venus. Karena ketiga objek tersebut membentuk sebuah segitiga, maka dengan menggunakan trigonometri, dua sudut dan ditambah satu sisi (Bumi-Venus) yang sudah diketahui bisa digunakan untuk menghitung salah satu sisi lainnya (Bumi-Matahari). Namun hasil yang diperoleh Huygens tidak dapat diterima secara luas oleh ilmu astronomi, karena hasil tersebut didapatkan dengan asumsi ukuran venus sama dengan ukuran bumi, dan kebetulan saja tebakannya benar (ukuran venus tidak berselisih jauh dengan ukuran bumi).
Giovanni Cassini, pada tahun 1672, mencoba mengukur jarak Matahari dengan metode yang berbeda, yaitu paralaks planet Mars. Cassini yang berada di Paris dibantu rekan di French Guiana untuk mengamati Mars pada saat yang sama. Ketika hasil pengamatan keduanya dibandingkan, mereka mendapatkan paralaks Mars jika dilihat dari 2 lokasi tersebut. Dan akhirnya jarak Matahari pun bisa dihitung dengan cukup baik. Cassini menyimpulkan bahwa jarak matahari dari bumi ialah sekitar 98 juta mil, masih kurang akurat jika dibandingkan dengan jarak yang kita ketahui saat ini, namun sudah mulai
mendekati.
mendekati.
Seiring berkembangnya teknologi, jarak Matahari semakin bisa diketahui secara lebih detil dan lebih akurat. Misalnya dengan menggunakan metode transit Venus atau Merkurius. Atau dengan menembakkan gelombang radio ke Venus, lalu menghitung selisih waktu penembakan dan penerimaan pantulannya. Dan sekarang kita ketahui bahwa jarak matahari dari bumi ialah 149.597.870.700 m. Jarak yang sangat jauh jika kita bandingkan dengan hasil penelitian terdahulu FE (5000 – 6000 km). Dengan jarak tersebut, cahaya dari Matahari dapat mencapai Bumi dalam waktu 8 menit 19 detik.
Berikut daftar hasil penelitian jarak matahari dari bumi yang pernah dilakukan para ilmuwan astronomi dengan menggunakan beberapa metode
| Nama | Tahun | Nilai Jarak | Metode |
| Hipparchos | 130 | 5 juta mil | Bayangan Bumi di Bulan |
| Cassini | 1672 | 98 juta mil | Paralaks Mars |
| Various | 1761 | 109 juta mil | Transit Venus |
| Various | 1769 | 88 juta mil | Transit Venus |
| Foucault | 1862 | 92 juta mil | Kecepatan cahaya |
| Hall | 1862 | 92 juta mil | Paralaks Mars |
| Stone | 1862 | 92 juta mil | Paralaks Mars |
| Various | 1874 | 91,7 juta mil | Transit Venus |
| Houzeau | 1882 | 92,7 juta mil | Transit Venus |
| Harkness | 1889 | 92.797.000 mil | Transit Venus 1761-1882 |
| Jones | 1941 | 91,5 juta mil | Paralaks asteroid Eros |
| Various | 1960 | 92.670.000 mil | Gerak satelit Pioneer 5 |
| NASA/JPL | 1961 | 92.955.820 mil,
149.597.519 km
| Radar Venus |
| Astronomi Moderen | 2009 | 92.955.807 mil,
149.597.870,7 km
| Telemetri |
Nah itulah sedikit yang dapat kami sampaikan mengeani perhitungan jarak Bumi dengan Matahri yang sedikit rumit. Semoga bisa sedikit mempercerah pikiran kita semua, terutama yang awam dengan ilmu fisika.
Hampir setiap hari kita melihat Matahari terbit dan tenggelam, kecuali pada saat langit sedang mendung. Seberapa jauh sih Matahari dari Bumi? Mungkin itu yang membuat kamu bertanya-tanya ya. Jawaban yang paling singkat adalah 1 AU (Astronomical Unit).
Orang yang pertama kali mencoba menghitung jarak Matahari dari Bumi secara kasar adalah Aristarchus, sekitar 2.250 tahun yang lalu, dengan menggunakan trigonometri ini pelajaran waktu SMP
Orang yang pertama kali mencoba menghitung jarak Matahari dari Bumi secara kasar adalah Aristarchus, sekitar 2.250 tahun yang lalu, dengan menggunakan trigonometri ini pelajaran waktu SMP
Belakangan, tepatnya pada tahun 1653, seorang astronom bernama Christiaan Huygens menghitung lagi jarak Matahari dari Bumi dengan teliti, dengan menggunakan metode triangulasi yang melibatkan Matahari, Bumi dan Venus. Hasil perhitungan Huygens dikoreksi lagi oleh Giovanni Cassini pada tahun 1672, dengan menggunakan metode paralaks, yang memuat perhitungan sudut secara lebih teliti.
Bagaimana sebenarnya cara astronom untuk dapat menghitung dan mengetahui jarak diantara benda-benda langit seperti Matahari, planet, bintang, galaksi dan sebagainya. Metode penentuan jarak bintang dan objek luar angkasa lainnya yang paling sederhana adalah metode paralaks trigonometri. Akibat perputaran Bumi mengitari Matahari, maka bintang-bintang yang dekat tampak bergeser letaknya terhadap latar belakang bintang-bintang yang jauh. Dengan mengukur sudut pergeseran itu (disebut sudut paralaks), dan karena kita tahu jarak Bumi ke Matahari, maka jarak bintang dapat ditentukan.
Pada abad ke-19 dilakukan pengukuran jarak bintang dengan cara Paralaks Trigonometri. Untuk memahami cara ini, lihatlah gambar berikut ini.

Akibat pergerakan Bumi mengelilingi Matahari, bintang terlihat seolah-olah bergerak dalam lintasan elips yg disebut elips paralaktik. Sudut yg dibentuk antara Bumi-bintang-Matahari (p) disebut paralaks bintang. Makin jauh jarak bintang dengan Bumi maka makin kecil pula paralaksnya. Dengan mengetahui besar paralaks bintang tsb, kita dapat menentukan jarak bintang dari hubungan:
tan p = R/d
R adalah jarak Bumi – Matahari, dan d adalah jarak Matahari – bintang. Karena sudut theta sangat kecil persamaan di atas dpt ditulis menjadi
Ø= R/d
pada persamaan di atas p dlm radian. Sebagian besar sudut p yg diperoleh dari pengamatan dlm satuan detik busur (lambang detik busur = {”}) (1 derajat = 3600″, 1 radian = 206265″).
Oleh krn itu bila p dalam detik busur, maka
p = 206265 (R/d)
Bila kita definisikan jarak dalam satuan astronomi (SA) (1 SA = 150 juta km), maka
p = 206265/d
Dalam astronomi, satuan jarak untuk bintang biasanya digunakan satuan parsec (pc) yg didefinisi sebagai jarak bintang yg paralaksnya satu detik busur. Dengan begini, kita dapatkan
1 pc = 206265 SA = 3,086 x 10^18 cm = 3,26 tahun cahaya
p = 1/d –> p dlm detik busur, dan d dlm parsec.
Dari pengamatan diperoleh bintang yg memiliki paralaks terbesar adalah bintang Proxima Centauri yaitu sebesar 0″,76.
Dengan menggunakan persamaan di atas maka jarak bintang ini dari Matahari (yg berarti jarak bintang dgn Bumi) adalah 1,3 pc = 4,01 x 10^13 km = 4,2 tahun cahaya (yang berarti cahaya yg dipancarkan oleh bintang ini membutuhkan waktu 4,2 tahun untuk sampai ke Bumi).
Sebarapa jauhkah jarak tersebut??
Bila kita kecilkan jarak Bumi – Matahari (150 juta km) menjadi 1 meter, maka jarak Matahari ke Proxima Centauri menjadi 260 km ,Karena sebab inilah bintang hanya terlihat sebagai titik cahaya walau menggunakan teleskop terbesar di observatorium Bosscha.
Sebenarnya ada beberapa cara lain untuk mengukur jarak bintang, seperti paralaks fotometri yg menggunakan kuat cahaya sebenarnya dari bintang. Kemudian cara paralaks trigonometri ini hanya bisa digunakan untuk bintang hingga jarak 200 pc saja. Untuk bintang2 yg lebih jauh, jaraknya dapat ditentukan dengan mengukur kecepatan bintang tersebut.
Perhitungan jarak bumi ke matahari ini didasarkan pada perhitungan kecepatan cahaya matahari sampai ke bumi dengan kecepatan rata-rata sekitar 8,3 menit.
keterlambatan ini bisa dihitung dari panjang gelombang sinar matahari yaitu ultra-violet yang bergeser beberapa nanometer dari panjang gelombang yang dihasilkan oleh proses termonuklir
kita tahu bahwa cahaya matahari terlambat 8.3 menit* dan kecepatan cahaya adalah 3x10^8 m/s sehingga jarak tempuhnya adalah:
Jarak Matahari = 8.3 x 60 x 3x10^8 m
Jarak Matahari = 149 000 000 km
Jadi jangan beranggapan Jika Ilmuwan cuma ngasal dalam perhitungan karena ditinjau dari namanya mereka pasti orang ber-Ilmu.
Metode Aristarchus
Elo bakalan kaget, gak? kalo gue bilang bahwa perjalanan manusia mengukur jarak antara bumi dan matahari dimulai sekitar 250 tahun sebelum masehi? That is the truth! Aristarchus (310-230 SM) tercatat dalam sejarah sebagai manusia pertama yang mencoba mengukur jarak matahari dari bumi.
Teori-teori yang disampaikan Aristarchus ini keren banget, mengingat beliau ada pada saat ilmu pengetahuan masih baru banget berkembang. Dari karya-karya beliau yang masih bisa dibaca, Aristarchus memprediksi bahwa pusat dari tata surya adalah Matahari. Tentu teori beliau masih sekitar 1800 tahun terlalu dini sampai dikorek oleh Nicholas Copernicus hingga menjadi sebuah teori astronomi yang paten. Tapi, karya beliau yang paling dikenal adalah perhitungan jarak antara Matahari dari Bumi.
Sebelum kita mulai mengupas persamaan yang dirangkai Aristarchus, lo harus paham dulu bahwa jarak Matahari dari Bumi berubah setiap detiknya. Iya karena rotasi dan revolusi Bumi. 1 AU yang kita liat diatas itu merupakan jarak rata-rata dihitung dari orbit terjauh Bumi dari Matahari (Aphelion) dan orbit terdekat Bumi dari Matahari (Perihelion).
Aristarchus ini adalah salah satu astronom di zaman Yunani kuno. Dia lahir tahun 320 Sebelum Masehi. Bisa bayangin itu setua apa? Sekitar 2200 tahun sebelum Indonesia merdeka, 1600 tahun sebelum Majapahit, dan 700 tahun sebelum kerajaan Kutai (kerjaan pertama di Nusantara). Pada zaman itu, tentu ga ada yang bisa bikin roket ke luar angkasa untuk mengukur jarak dari matahari ke bumi. Terus gimana cara Aristarchus ini bisa mengukur jaraknya?
Okay, sebenernya Aristarchus ini belum benar-benar mengukur jarak dari matahari ke bumi. Yang dia lakukan itu cuma mengukur perbandingan antara jarak bumi-matahari dan bumi-bulan. Dia melakukan pengukuran ini ketika bulan tampak setengah lingkaran dari bumi. Wah, gimana caranya tuh?
Nah, sebelum lu scroll ke bawah, coba pikir dulu, kira-kira gimana metode dia untuk mengukur perbandingan jarak Bumi-Matahari dan Bumi-Bulan ketika bulan tampak setengah lingkaran. Petunjuknya: Gambar posisi Bulan, Matahari, dan Bumi ketika bulan tampak setengah lingkaran. Contohnya seperti gambar Bulan berikut ini. 

Okay, gue lanjutin ya.
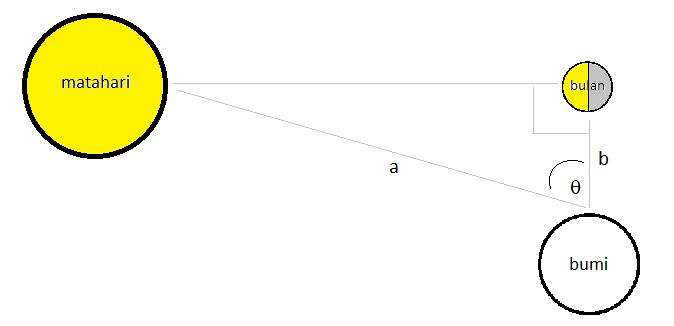
Ketika bulan tampak setengah lingkaran dari permukaan bumi, maka matahari, bulan, dan bumi akan membentuk sudut tegak lurus seperti gambar berikut ini:
Okay, perlu gue tekankan bahwa gambar di atas itu simplifikasi dari posisi sebenarnya,ya. Harusnya matahari itu jauh lebih besar dari pada bumi dan bulan, sudut θ juga harusnya ga setajam itu, tapi mendekati 90 derajat. Tapi penggambaran ini ga jauh beda dengan apa yang dilakukan oleh Aristarchus.
Nah, untuk bisa mendapatkan perbandingan antara b dengan a, kira-kira apa yang harus dilakukan oleh Aristarchus? Dia tinggal menghitung sudut θ!
Menghitung sudut bulan-bumi-matahari (sudut θ)
Teknik yang dilakukan oleh Aristarchus untuk menghitung sudut θ ini ga jauh berbeda dengan yang dilakukan oleh Eratosthenes.
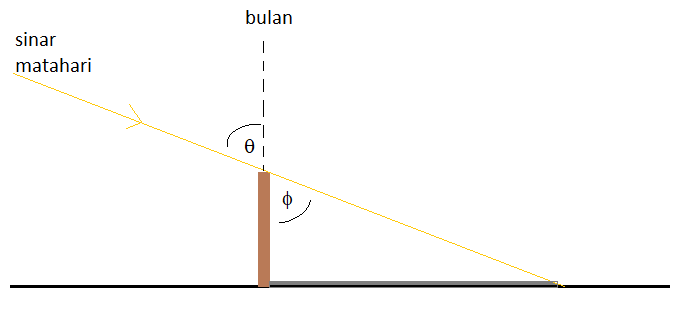
Aristarchus tinggal meletakkan sebuah tongkat secara tegak ketika bulan itu berada tepat di atasnya, seperti gambar di atas. Berikutnya, dia bisa mengukur bayangan yang terbentuk akibat adanya sinar matahari di atas. Sudut ɸ bisa dicari dengan persamaan:
tan ɸ = Panjang bayangan / Panjang tongkat
Berhubung sudut ɸ dan sudut θ saling bertolak belakang, maka kita bisa menyimpulkan bahwa:
θ = ɸ
Hore! Aristarchus berhasil menghitung sudut antara bulan-bumi-matahari!
Perbandingan jarak bumi-bulan dengan bumi-matahari
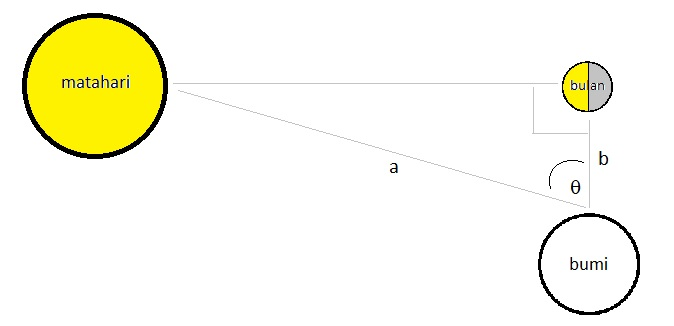
Setelah sudut θ diketahui, perbandingan antara b dengan a pada gambar di atas tentu gampang dicari dong, ya? Yup, langsung aja:
Cos θ = b/a
Nah, Aristarchus melakukan hal di atas dan menemukan bahwa sudut θ itu besarnya adalah 87o. Tinggal kita masukkan ke persamaan, deh:
Cos 87o = 1/19
Wah, berarti dapet nih! Perbandingan jarak bumi-bulan dengan bumi-matahari adalah 1:19! Aristarchus pun senang. 

Eh tunggu! Kok udah pakai Trigonometri sih? Emangnya di zaman Yunani kuno, Trigonometri sudah ditemukan?
Okay, tentu Trigonometri yang kita kenal sekarang dengan nama-nama yang sok asik itu (sin, cos, tan) belum dikenal. Tapi konsep perbandingan segitiga siku-siku itu udah dikenal pada zaman Yunani kuno. Jadi ketika Aristarchus itu menemukan bahwa sudut yang harus dia cari perbandingannya adalah 87o misalnya, dia tinggal menggambar suatu segitiga siku-siku yang salah satu sudutnya adalah 87o. Setelah itu, dia ukur perbandingan antara sisi samping dengan sisi miringnya. Jadi dia ga perlu tahu tentang cosinus untuk bisa melakukan hal ini karena Trigonometri pun konsep dasarnya adalah dari perbandingan segitiga.
Perhitungannya Aristarchus ini akurat ga sih?
Meskipun metodenya Aristarchus ini menarik, tapi sayangnya hasil perhitungan dia sangat jauh dari ukuran yang sebenarnya. Menurut perhitungan modern, sudut sebenarnya itu bukan 87o, tapi 89,83o. Kalau kita masukkan ke dalam cosinus, hasil perhitungannya adalah 1:400. Jauh banget ya.
Supaya dia nggak sedih, gimana kalau kita bilang ke Aristarchus, “Ga apa-apa kok, Aristarchus! Aku tetap bangga sama kamu!”
Anyway, meskipun belum akurat, tapi belum ada yang berhasil mengoreksi perhitungan Aristarchus ini sampai 1900 tahun kemudian loh! Sudut pengukuran Aristarchus ini kemudian diperbaiki oleh Godefroy Wendelin.
Temuan Wendelin & Horrocks
Pada abad ke-17, seorang astronom dari Flandria (sekarang merupakan bagian dari Belgia) bernama Godefroy Wendolinmenggunakan teleskop untuk mengoreksi observasi sudut yang terbentuk diantara Bulan-Bumi-Matahari. Dengan kata lain, paman Wendolin mengoreksi metode Aristarchus. Ia juga memetakan lokasi bintang yang tersebar di angkasa.
Beliau mengamati bahwa besar sudut tersebut bukanlah 87o namun 89,7o-89,75 o. Dengan koreksi tersebut maka kita dapat mengubah persamaan kita diatas tadi dan mendapatkan bahwa perbandingan jarak antara Bumi ke Bulan dan Bumi ke Matahari sebenernya mencapai 1 berbanding 220.
Wow. Sekarang kita udah deket banget dengan nilai perbandingan jarak yang sebenarnya yaitu sekitar 1 berbanding 400.
Selang 4 tahun kemudian, Jeremiah Horrocks (seorang astronom dari Inggris) menemukan metode lain untuk mengukur jarak antara Bumi dan Matahari. Untuk mengukur jarak tersebut beliau menggunakan posisi relatif Venus terhadap Matahari. Perhitungan Horrocks dilakukan dengan pengamatan terhadap Venus dari berbagai tempat di Bumi.
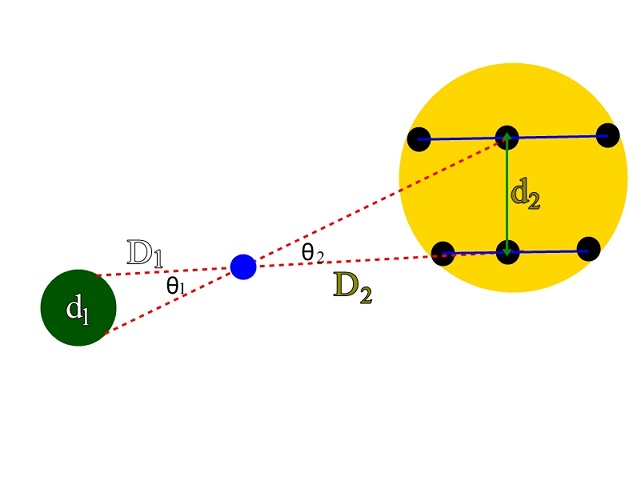
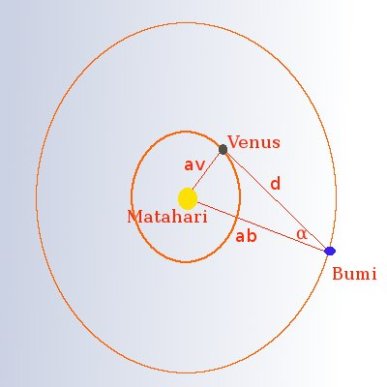
Untuk memahami metode Horrocs, kita coba buat datanya lebih simpel dengan menaruh pengamatan pada dua titik saja. Coba perhatikan ilustrasinya.
Nah, dari kedua lokasi tersebut, dilakukan pengamatan terhadap posisi Venus ketika posisi orbitnya dapat diamati dari Bumi. Posisi Venus ketika mengorbit Mataharinya pun diamati tidak hanya sekali saja. Kemudian Horrocs dapat memperhitungkan secara kasar berapa jarak d2 dengan menggunakan geometri.
Dengan menggunakan hubungan sudut, diketahui bahwa θ1 dan θ2 besarnya sama. Kemudian dengan menggunakan nilai sin untuk sudut yang sangat kecil, diperoleh bahwa perbandingan d1/D1 sama dengan d2/D2. Dengan ilustrasi tersebut Horrocks juga dapat memperoleh estimasi jarak antara Bumi ke Matahari yaitu sekitar 144,840,960 km. Perhitungan beliau meleset sekitar 10 juta kilometer tapi nilai ini udah bagus banget.
Metode Parallax

Metode berikutnya adalah sebuah metode yang dinamakan Metode Parallax. Metode ini digunakan oleh seorang yang bernama Giovanni Cassini. Ia menjadi orang pertama yang bisa memberikan nilai yang cukup akurat mengenai jarak antara Matahari ke Bumi. Bagaimana Cassini bisa mendapatkan angka tersebut? Dengan mengukur jarak antara Bumi dan Mars. Loh? Iya, doi ngukur jarak antara Bumi dan Mars dulu, abis itu baru dia ngukur jarak antara Bumi dan Matahari.
Gini ceritanya. Pada tahun 1672, Cassini menggunakan sebuah alat yang biasanya digunakan oleh pelaut untuk navigasi. Kecuali elo bajak laut atau pelaut mungkin elo nggak akan familiar dengan alat ini. Nama alatnya itu sextant. Ini aksesoris yang ditempel pada teleskop. Bentuknya kayak gini.

Bentuknya mirip busur, ya? Nah, alat yang di bawahnya ini bisa ngukur nilai sudut yang cukup akurat. Jauh lebih akurat daripada ngukur sudut pake tongkat atau teleskop. BTW, sebenernya metode yang digunakan oleh Cassini ini sempat terlebih dahulu digunakan oleh seseorang bernama Huygens. Akan tetapi, banyak asumsi yang digunakan Huygens meleset sehingga Huygens dinyatakan tidak ilmiah. Maka Cassini dinyatakan sebagai penggagas metode yang biasa disebut sebagai Parallax.
Nama mereka digunakan untuk dijadikan satelit yang digunakan untuk mempelajari Saturnus. Cassini-Huygens nama satelit buatannya, namun lebih dikenal dengan sebutan satelit Cassini. Kasian deh Huygens, nggak saintifik sih lo. Satelit ini merupakan satelin pertama yang berhasil memasuki orbit Saturnus.

Eksperimen untuk Mencari Sudut Parallax
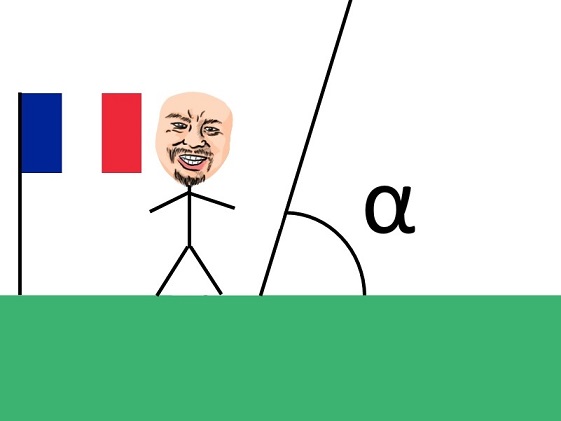
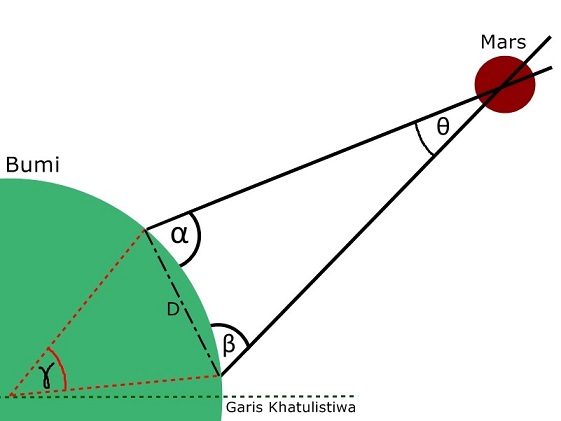
Sekarang kita bakal ngomongin bagian serunya nih. Huehehhe. Ekseperimen ini dilakukan Cassini dengan mengukur sudut yang terbentuk antara Mars dan Bumi dari dua sudut pandang berbeda. Nah yang gue jelasin di sini itu versi sederhana dari eksperimennya yah. Kalo aslinya, Cassini ngumpulin data segambreng dulu. Jadi dapat hasil rata-ratanya. Cassini melakukan pengukuran dari 2 tempat, yaitu Perancis dan Guyana Perancis (French Guyana).
Di Paris, Perancis, Cassini mendapatkan sudut alpha sebagai berikut:
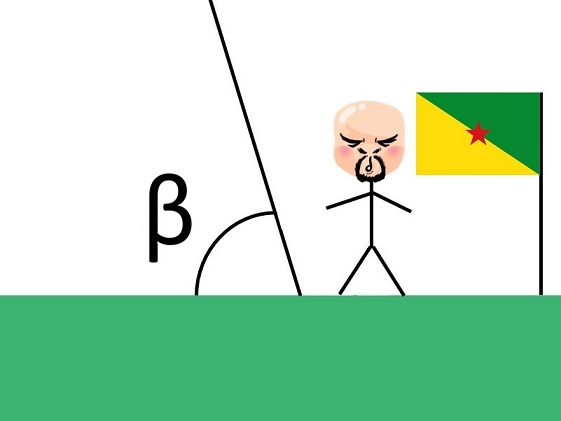
Kemudian Cassini mengirim seorang kolega bernama John Richer untuk mengukur di Guyana Perancis. Guyana Perancis ini lokasinya ada di Amerika Selatan, ya. Kemudian, Richer mendapatkan sudut beta sebagai berikut:
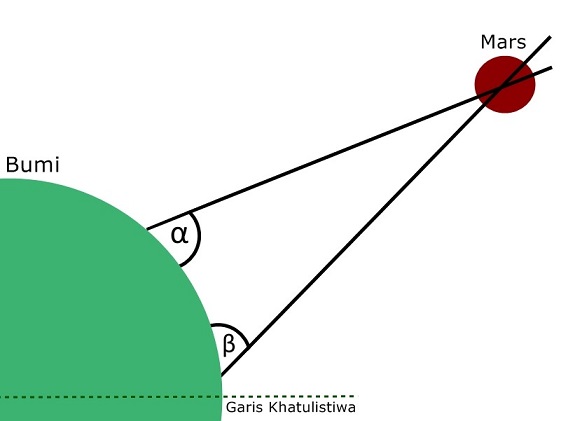
Begitulah wajah Richer yang bete, soalnya harus keluar dari zona nyaman di Eropa dan menjelajah Amerika Selatan duluuntuk memperoleh data. Anyway, kalau kedua gambar itu kita zoom out, maka sudut alpha dan beta itu menjadi seperti ini:
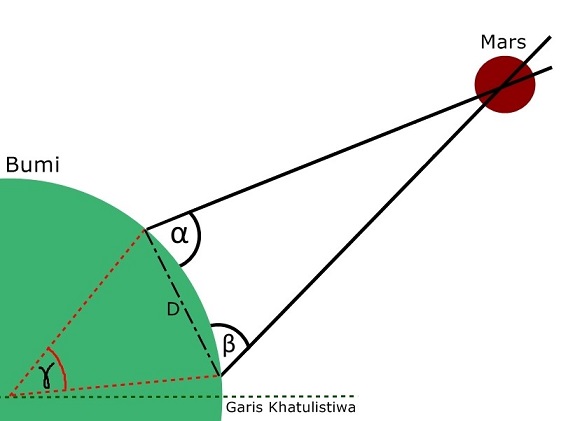
Berhubung mereka bisa mengetahui posisi Paris dan Guyana Perancis dengan menghitung sudut ke matahari, maka mereka bisa tahu sudut gamma di bawah ini:
Nah, sudut Parallax yang mau mereka cari itu adalah sudut theta di bawah ini:
Sekarang elo gue kasih puzzle, nih (biar kesannya bukan soal) biar lebih rame dan seru. Kalau alpha, beta, gamma sudah diketahui, gimana cara mencari sudut thetanya? Nih biar kebayang gue kasih angka (ini bukan nilai sebenarnya yah):
Misalkan besar sudut α = 75o. Terus sudut β besarnya 70o. Besar sudut γ itu 25o. Berapa coba nilai sudut θ (Parallax-nya )? Silakan jawab di kolom komentar, ya.
Kalo elo bingung gimana nyelesaiin puzzle-nya, nih gue kasih clue.
Jarak Bumi-Mars
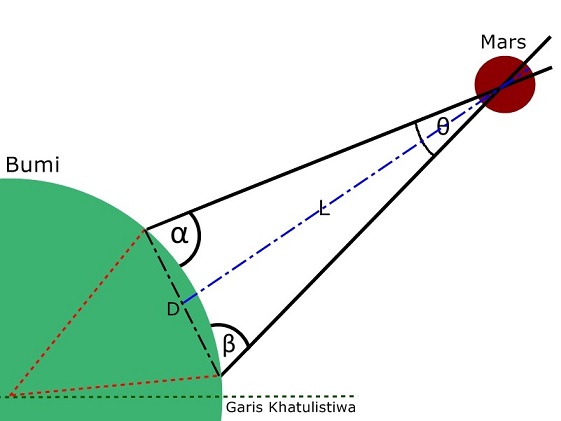
Nah, kalau sudut parallax sudah diketahui, gimana cara Cassini menghitung jarak dari Bumi ke Mars? Kita gambar lagi yah.
Puzzle terakhir nih terakhir. Tapi elo bakal paham, nih gimana cara ngitung jarak ke Mars.
Misalkan D itu besarnya 7.000 km. Kemudian misalkan sudut parallaxnya adalah 10o. Berapakah nilai L? (tulis jawaban lu di comment lagi ya)
Sekali lagi kalo elo bingung, lo bisa cek artikel yang gue kasih tadi.
Seru kan? Iseng-iseng berhadiah ilmu pengetahuan *tsaaah. Sekali lagi gue ingatkan nilai yang gue kasih di puzzle tadi, tuh, bukan nilai sebenarnya, yah. Sudut parallax itu aslinya nilainya nol koma sekian derajat. Kecil banget nilainya. Jadi nanti nilai L yang didapet yah gede banget juga, men.
Jarak Bumi-Matahari
Cassini sudah bisa menghitung jarak Bumi-Mars, tapi kan yang mau kita cari adalah jarak Bumi-Matahari. Jeng jeng. Ternyata belum selesai yah. Kebetulan, Astronom sebelum Cassini sudah bisa mengetahui jarak Mars ke Matahari (ini ga kita bahas di sini ya karena kepanjangan). Kemudian, Cassini juga bisa mengukur sudut Mars-Bumi-Matahari, sebut aja sudut θ. Hati-hati ketuker dengan θ yang sudut parallax tadi yah. Kalau kita gambarkan ketika benda langit tersebut, gambarnya jadi begini:
Okay, kalau kita tahu besar L, x, dan theta, gimana cara menghitung p? Nih gue kasih angkanya lagi:
Diketahui nilai dari x adalah 228 km dan nilai dari L adalah 55 km. Sudut θ diketahui sebesar 60o Berapakah nilai p? (tulis jawaban di komentar di bawah ya)
Clue-nya juga ada di artikel tadi, ya.
Bagaimana dengan Perhitungan di Era Modern?
Meski nilai yang diperoleh oleh Cassini memang tidak seratus persen akurat, yaitu meleset sekitar 6% dari nilai yang kita dapat dari hasil eksperimen di abad 21. Namun, untuk tepat dugaan lo. Nilai yang kita punya masih merupakan hasil suatu perhitungan dan mungkin saja dalam beberapa waktu ke depan seiring dengan berkembangnya ilmu pengetahuan, akan terjadi koreksi lagi terhadap nilai AU.
Di era modern ini, jika kita ingin melakukan perhitungan jarak antara Bumi dan benda langit lainyya, kita bisa memanfaatkan teknologi seperti satelit. Pengukuran dilakukan dengan mengirimkan satelit mendekati benda langit yang ingin kita ukur jaraknya. Setelah itu yang perlu kita lakukan adalah mengirimkan sinyal pada satelit tersebut dan menunggu waktu terpantulnya sinyal tersebut oleh satelit sampai kembali ke Bumi.
Keren, yah. Ternyata pertanyaan-pertanyaan yang mungkin tidak pernah terbayangkan untuk bisa dijawab oleh manusia dapat dicari jawabannya dengan metode yang simpel. Dengan geometri yang cukup sederhana dan pengetahuan untuk mengukur sudut, kita dapat mengukur berbagai hal seperti jarak dan diameter dari beragam benda langit yang ada di alam semesta.
So, jangan pernah sekalipun menggantung mimpimu hanya setinggi pohon mangga, apalagi pohon toge. Gantungkan mimpimu setinggi langit. Bahkan Matahari yang belum mencapai ujung langit saja berjarak 149.597.870.700 meter dari Bumi yang kita pijak. Siapa tahu dalam 30 tahun kedepan elo akan menjadi orang Mars pertama? Berarti elomenggantungkan cita-cita lo setinggi 229 juta kilometer.
Anyway, sekian dulu pembahasan dari kami. Semoga tulisan ini bisa menginspirasi lo untuk terus menggali ilmu tentang alam semesta. To quote Buzz Lightyear, to infinity and beyond!
[https://www.youtube.com/watch?v=vqtqiqWqXmI]
Tentang metode Aristarchus yang ngukur pertama kali [http://www.astro.cornell.edu/academics/courses/astro201/aristarchus.htm]
Metode perbaikan Jeremiah Horrocks
[http://www.staff.science.uu.nl/~gent0113/venus/venus_text17.htm]
[http://www.staff.science.uu.nl/~gent0113/venus/venus_text17.htm]
History of using parallax
[https://spaceplace.nasa.gov/review/dr-marc-solar-system/planet-distances.html] [https://www.space.com/17081-how-far-is-earth-from-the-sun.html]
[https://spaceplace.nasa.gov/review/dr-marc-solar-system/planet-distances.html] [https://www.space.com/17081-how-far-is-earth-from-the-sun.html]
Angle of Parallax
[https://www.space.com/30417-parallax.html] [https://www2.jpl.nasa.gov/teachers/attachments/parallax.html]
[https://www.space.com/30417-parallax.html] [https://www2.jpl.nasa.gov/teachers/attachments/parallax.html]
jarak bumi ke matahari tahun cahayajarak matahari ke bumi disebutbulan jarak ke bumi
cara menghitung jarak planet ke matahari
sirius jarak ke bumi
cara mengukur matahari
jarak matahari dan bumi sekarangjarak matahari ke bulanjarak bumi ke matahari tahun cahayajarak matahari ke bumi disebutbulan jarak ke bumi
cara menghitung jarak planet ke matahari
sirius jarak ke bumi
cara mengukur matahari
jarak matahari dan bumi sekarangjarak matahari ke bulan
jarak bumi ke matahari tahun cahaya
jarak matahari ke bumi disebutbulan jarak ke bumi
cara menghitung jarak planet ke matahari
sirius jarak ke bumi
cara mengukur matahari
jarak matahari dan bumi sekarangjarak matahari ke bulanjarak bumi ke matahari tahun cahayajarak matahari ke bumi disebutbulan jarak ke bumi
cara menghitung jarak planet ke matahari
sirius jarak ke bumi
cara mengukur matahari
jarak matahari dan bumi sekarangjarak matahari ke bulan
jarak bumi ke matahari tahun cahayajarak matahari ke bumi disebutbulan jarak ke bumi
cara menghitung jarak planet ke matahari
sirius jarak ke bumi
cara mengukur matahari
jarak matahari dan bumi sekarangjarak matahari ke bulanjarak bumi ke matahari tahun cahayajarak matahari ke bumi disebutbulan jarak ke bumi
cara menghitung jarak planet ke matahari
sirius jarak ke bumi
cara mengukur matahari
jarak matahari dan bumi sekarangjarak matahari ke bulan
jarak bumi ke matahari tahun cahayajarak matahari ke bumi disebutbulan jarak ke bumi
cara menghitung jarak planet ke matahari
sirius jarak ke bumi
cara mengukur matahari
jarak matahari dan bumi sekarangjarak matahari ke bulanjarak bumi ke matahari tahun cahayajarak matahari ke bumi disebutbulan jarak ke bumi
cara menghitung jarak planet ke matahari
sirius jarak ke bumi
cara mengukur matahari
jarak matahari dan bumi sekarangjarak matahari ke bulan
cara menghitung jarak planet ke matahari
sirius jarak ke bumi
cara mengukur matahari
jarak matahari dan bumi sekarangjarak matahari ke bulanjarak bumi ke matahari tahun cahayajarak matahari ke bumi disebutbulan jarak ke bumi
cara menghitung jarak planet ke matahari
sirius jarak ke bumi
cara mengukur matahari
jarak matahari dan bumi sekarangjarak matahari ke bulan
Advertisement